Abstract
Selective fluorination of the pyrrolidine ring in proline motifs has been found to induce significant conformational changes that impact the structure and biological roles of modified peptides and proteins. Vicinal difluorination of fluoroproline, for example, in (3S,4R)-3,4-difluoroproline, serves to mitigate the inherent conformational bias of the pyrrolidine ring by inducing stereoelectronic effects that attenuate this conformational bias. In this investigation, we present a quantumchemical analysis of the conformational equilibrium and effects that are induced in difluorinated pyrrolidines, with a particular focus on exploring the impact of gauche and anomeric effects on the conformer stabilities of different stereo- and regioisomers. Initially, we conducted a benchmark assessment comparing the optimal density functional theory method with coupled cluster with single and double excitations (CCSD) calculations and crystallographic data using the 3-fluoropyrrolidinium cation and 3-fluoropyrrolidine. Subsequently, we explored the relative energy of all favored conformations of all different stereoisomers of 2,3-, 2,4-, and 3,4-difluoropyrrolidines at the B3LYP-D3BJ/6-311++G** level. A generalized anomeric effect, arising from nN→σ*CF electron delocalization, is particularly important in modulating the energetics of the α-fluoro isomers and imparts a strong conformational bias. In contrast, the fluorine gauche effect assumes a secondary role, as it is overshadowed by steric and electrostatic interactions, referred to as Lewis interactions from a natural bond orbital perspective.
Graphical Abstract
Introduction
The pyrrolidine ring structure is prevalent in numerous natural alkaloids and is an important feature of the proline and hydroxyproline residues that pervade biochemistry in peptides and proteins. The chemical and biological properties of substituted pyrrolidine derivatives, along with many other compounds, hinge on the relative stereochemistry. It is well established that the presence of fluorine in an organic molecule can significantly influence the stereochemical behavior. Consequently, various molecular properties, such as polarity, viscosity, and intra- and intermolecular interactions, are impacted by the C‒F bond. These features underlie the important role of selective fluorination in pharmaceuticals and agrochemicals development [1].
For instance, substituted 3-fluoropyrrolidines, particularly in the form of 2-carboxy derivatives (fluoroprolines), have been extensively explored. These compounds represent valuable nonnatural amino acids, and depending on the regio- and stereochemistry of fluorine substitution, fluoroproline substututions can enhance the conformational stability of proline-rich proteins such as collagen [2]. Therefore, pyrrolidine derivatives are particularly susceptible to conformational control induced by a fluorine substituent.
The 5-membered pyrrolidine ring is a cyclic alkylamine that adopts a conformation that resembles the familiar envelope of cyclopentane, with an NH unit occupying either a pseudoaxial or pseudoequatorial position (Figure 1a). When a hydrogen atom of the pyrrolidine at C-3 is replaced with fluorine, a conformational interconversion can occur within the cis- and trans-isomers, as illustrated in Figure 1b. The fluorine gauche effect, commonly observed in compounds containing the F‒C‒C‒X fragment (where X is an electron-withdrawing substituent, such as nitrogen), typically favors a conformation where F and X are gauche to each other. This preference is attributed to stabilizing σCH→σ*CF and σCH→σ*CX hyperconjugative interactions [3]. However, it is noteworthy that 3-fluoropiperidine does not exhibit such a fluorine gauche effect. In this case, the axial conformer is similarly populated to the equatorial conformer, despite the favorable antiperiplanar arrangement of orbitals that would facilitate these interactions [4].
Figure 1: a) Pseudoequatorial and pseudoaxial conformations of pyrrolidine. b) Cis- and trans-isomers of 3-fluoropyrrolidine.
Figure 1: a) Pseudoequatorial and pseudoaxial conformations of pyrrolidine. b) Cis- and trans-isomers of 3-fl...
Protonation of 3-fluoropyrrolidine generates the 3-fluoropyrrolidinium cation, and this typically results in a highly favored conformation in both the gas phase and solution where the fluorine and nitrogen atoms are cis, mirroring the behavior observed in analagous 4- and 6-membered ring systems [5]. This conformational preference is attributed to an electrostatic gauche effect, where an attractive NH2+∙∙∙Fδ− interaction reinforces the well-known hyperconjugative gauche effect. Additionally, NH∙∙∙F hydrogen bonding has been proposed to play a role in stabilizing conformers of certain 3-fluoroalkylamines and the respective cations [6].
Intramolecular hydrogen bonds involving either the carboxy or hydroxy group of 4R- and 4S-hydroxyproline have been identified as key factors in stabilizing the favored conformations in the gas phase. Therein, the contribution of a gauche effect due to electron delocalization is considered to be secondary [7]. However, stabilization via intramolecular hydrogen bonding does not seem to significantly impact the conformational stability of 3-fluoropiperidine. In this context, the cis-conformer, with the axial fluorine atom facing the N-hydrogen atom, is either equally or only slightly more stable than the other three conformers in both the gas phase and implicit water [4]. Hence, it appears that strong intramolecular interactions, and not only hydrogen bonding, govern the orientation of the fluorine atom in the F‒C‒C‒N fragment, favoring the cis-isomer of 3-fluoropyrrolidine.
To investigate potential changes in the preferred orientation of the fluorine substituent in 3-fluoropyrrolidine and the respective cation, an additional fluorine atom was introduced into the molecule for theoretic studies (Figure 2). The subsequent evaluation focused on the role of anomeric and fluorine gauche effects to evaluate significant conformational biases in all of the possible isomers.
Figure 2: Flat representations of 2,3-, 3,4-, and 2,4-difluoropyrrolidines. The potential effects resulting from the addition of a second 1,2- or 1,3-fluorine atom (nN→σ*CF anomeric and σCH→σ*CF fluorine gauche effects) on the conformation of different stereoisomers is explored.
Figure 2: Flat representations of 2,3-, 3,4-, and 2,4-difluoropyrrolidines. The potential effects resulting f...
Achieving conformational control upon the introduction of a second fluorine atom in fluoropyrrolidine presents challenges. Unlike the chair-like conformation of six-membered rings, five-membered rings lack the geometric arrangement necessary to most effectively accommodate anomeric and gauche effects [8,9]. It is noteworthy that vicinal difluorination has previously been demonstrated to minimize conformational bias in fluoroprolines [10], offering some insight into the potential outcomes of this study.
In this study, initially, the conformational equilibrium of 3-fluoropyrrolidine and the corresponding cation were analyzed to establish a benchmark for selecting an appropriate theory level for subsequent calculations. Then, the different isomers of the 1,2- or 1,3-difluorinated pyrrolidines were each be subjected to quantum-chemical analysis.
Results and Discussion
In order to achieve the most accurate conformational depiction of the difluorinated pyrrolidines through density functional theory (DFT), a benchmark study was conducted. This study compares the crystallographic geometry of a pyrrolidinium salt [11] with the CCSD/DGTZVP geometry of the pyrrolidinium cation (with an exclusively axial C–F bond) and the energy of 3-fluoropyrrolidine conformations. Various combinations of DFT methods (B3LYP-D3BJ, ωB97XD, and PBEPBE) and basis sets (DGTZVP and 6-311++G**) were evaluated. The selection of these functionals was based on whether or not they included dispersion terms that could influence the absolute energy. These functionals are widely used and have demonstrated strong performance in numerous evaluations and validations across the literature. Similarly, for the basis sets, a comparison was made between a triple-zeta valence plus polarization basis set with diffuse and tight d-functions (DGTZVP) and a Pople-based large basis set with polarizability and diffuse functions, often referred to as high standard.
The geometry was assessed based on atom distance, bond length, dihedral angle, etc. The analysis revealed that the lowest mean absolute error (MAE) [12] was observed for the B3LYP-D3BJ/6-311++G** and ωB97XD/6-311++G** levels (Figure 3). While there were differences between the CCSD and experimental structures, attributed to intermolecular forces and counterion effects, these differences did not impact the selection of the best levels based on geometry criteria.
![[1860-5397-20-140-3]](/bjoc/content/figures/1860-5397-20-140-3.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 3: MAE comparing the geometry parameters (bond length, bond angle, and dihedral angle) obtained from DFT calculations at the CCSD/DGTZVP level. The MAE for the crystal structure compared to the CCSD structure is 20.3316. “a” denotes DGTZVP and “b” denotes 6-311++G**.
Figure 3: MAE comparing the geometry parameters (bond length, bond angle, and dihedral angle) obtained from D...
Regarding the conformational energy, 3-fluoropyrrolidine exhibited four conformers in the gas phase, although this was reduced to three in implicit DMSO experiments (Table 1). In both cases, a cis-twist ring with an axial N–H bond was the most stable conformer, allowing for an intramolecular F∙∙∙H hydrogen bond. However, 3-fluoropyrrolidine displayed extensive conformational diversity (ΔG0 among conformers ≤1.6 kcal⋅mol−1) as the intramolecular interactions were not sufficiently stabilizing to dictate a dominant conformation. Consequently the introduction of a second fluorine atom with an appropriate relative configuration was thought to reinforce and establish a predominant conformation.
Table 1: Conformational energy (ΔG0, kcal⋅mol−1) and population (%) of 3-fluoropyrrolidine according to different theoretical levels for the gas phase and implicit DMSO (in parentheses), along with the MAE compared to the CCSD/DGTZVP level.
![[Graphic 1]](/bjoc/content/inline/1860-5397-20-140-i1.png?max-width=637&scale=1.0)
|
||||||||
| conformer | CCSD/aa | B3LYP-D3BJ/a | B3LYP-D3BJ/bb | ωB97XD/a | ωB97XD/b | PBEPBE/a | PBEPBE/b | average, % |
| NHaxFcis | 0.00 (0.00) | 0.00 (0.00) | 0.00 (0.00) | 0.00 (0.00) | 0.00 (0.00) | 0.00 (0.00) | 0.00 (0.00) | 54 (64) |
| NHaxFtrans | 1.00 (0.46) | 0.97 (0.47) | 0.94 (0.47) | 0.96 (0.49) | 0.91 (0.47) | 0.97 (0.51) | 0.96 (0.53) | 11 (28) |
| NHeqFcis | 0.28 (—) | 0.31 (—) | 0.28 (—) | 0.20 (—) | 0.09 (—) | 0.61 (—) | 0.56 (—) | 31 (—) |
| NHeqFtrans | 1.60 (1.17) | 1.59 (1.27) | 1.45 (1.09) | 1.57 (1.21) | 1.49 (1.07) | 1.64 (1.35) | 1.46 (1.15) | 4 (9) |
| MAE | — | 0.02 (0.04) | 0.05 (0.03) | 0.04 (0.02) | 0.10 (0.04) | 0.10 (0.08) | 0.12 (0.03) | — |
aa = DGTZVP. bb = 6-311++G**.
Theoretical levels that closely approximated the CCSD outcome included B3LYP-D3BJ/6-311++G**, B3LYP-D3BJ/DGTZVP, and ωB97XD/DGTZVP (Table 1). Consequently, the B3LYP-D3BJ/6-311++G** level was selected for further calculations involving the difluorinated pyrrolidines shown in Figure 4.
Figure 4: Exhaustive illustration of all conformational, configurational, and constitutional isomers of difluorinated pyrrolidine, illustrating the relative orientation of the C–F and N–H bonds used to build the input geometry for the calculations. The pairs 10/11 and 14/15 were degenerate. Consequently, only one structure of each pair was computed.
Figure 4: Exhaustive illustration of all conformational, configurational, and constitutional isomers of diflu...
From the pool of 24 potential conformational, configurational, and constitutional isomers of the difluorinated pyrrolidines (i.e., 1–24), two pairs were degenerate (i.e., 10/11 and 14/15), reducing the number of distinct structures to 22. However, due to the considerable flexibility of the five-membered ring and the low barrier for pyramidal interconversion of the N–H moiety, some inputs converged to the same isomer post-geometry optimization. Consequently, a total of 10 different structures was identified in the gas phase, with two additional structures observed in implicit DMSO (using solvation model density, SMD), bringing the total to 12.
Since the atomic composition of the compounds in Figure 4 was the same, the relative energy may be compared, and a stability landscape covering all optimized structures may be obtained from this analysis. Among these structures, only six were found to be significantly stable (<3 kcal⋅mol−1) in either the gas phase or DMSO. Remarkably, structure 19 was the most stable, followed by structure 17, as shown in Figure 5 and Table 2. This disparity in stability was largely attributed to the relative orientation of the nitrogen electron lone pair and the adjacent C–F bond, facilitating an anomeric interaction characterized by nN→σ*CF electron delocalization. Isomer 2 also demonstrated such an orientation, but the C–F bonds in this case were vicinal. Compounds lacking α-fluorine atoms (i.e., 9, 10, 12, and 16) possessed a notably higher energy, indicating the impact of the anomeric effect.
![[1860-5397-20-140-5]](/bjoc/content/figures/1860-5397-20-140-5.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 5: Stable difluorinated pyrrolidines derived from gas-phase calculations performed at the B3LYP-D3BJ/6-311++G** level. Conformers: 1/4, 2/3, 9/12, and 18/19. Stereoisomers: 1 /4, 9/12, and 17/19.
Figure 5: Stable difluorinated pyrrolidines derived from gas-phase calculations performed at the B3LYP-D3BJ/6...
Table 2: Relative Gibbs free energy (kcal⋅mol−1) for the geometry-optimized difluorinated pyrrolidines.
| isomer | ΔG0gas | isomer | ΔG0DMSO |
| 1 | 3.50 | 1 | 3.23 |
| 2 | 1.15 | 2 | 1.83 |
| 3 | 1.79 | 3 | 2.20 |
| 4 | 7.59 | 4 | 3.23 |
| 9 | 13.02 | 5 | 3.47 |
| 10 | 9.70 | 6 | 2.19 |
| 12 | 13.55 | 9 | 12.94 |
| 17 | 0.75 | 10 | 10.88 |
| 18 | 1.79 | 12 | 12.87 |
| 19 | 0.00 | 17 | 0.11 |
| 18 | 1.01 | ||
| 19 | 0.00 | ||
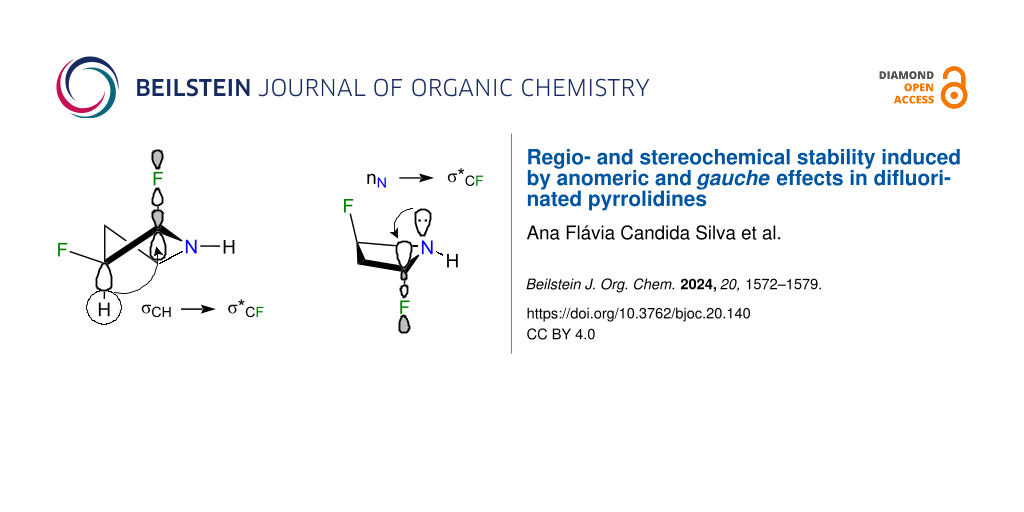
To further illuminate these findings, a natural bond orbital (NBO) analysis was conducted across the entire array of difluorinated pyrrolidines to assess the relative energy in isodesmic relationships (Table 3). Unlike in 1,2-difluoroethane [10,13], vicinal gauche-oriented fluorine atoms in 5-membered rings, particularly in compounds 1, 9, and 12, as well as in 6-membered rings, do not favor σCH→σ*CF interactions. Rather, less stabilizing σCC→σ*CF interactions were anticipated. Moreover, besides the anomeric interaction, the pseudoaxially oriented C–F bonds in 17 and 19 facilitated efficient electron donation from vicinal antiperiplanar C–H bonds through σCH→σ*CF interactions (Figure 6). The methylene group separating both C–F bonds in 17 and 19 enabled an additional σCH→σ*CF interaction, rather than the negligible σCF→σ*CF electron delocalization that would occur if these bonds were vicinally antiperiplanar. As discerned from the decomposition of the full electronic energy into Lewis (e.g., steric effects) and non-Lewis (electron delocalization) contributions, 17 and 19 were favored by a delicate equilibrium between weak repulsion and substantial stabilization due to hyperconjugation. Conversely, structures such as 9 and 10 experienced minimal steric effects but were inadequately stabilized by electron delocalization, rendering them higher in energy when compared to the other isomers. Compounds 1 and 4, with syn-C–F bonds, exhibited the highest ΔELewis term due to significant dipolar and steric repulsions.
Table 3: Relative electronic energy (ΔEfull = ΔELewis + ΔEnon-Lewis) in isodesmic relationships and significant electron delocalization derived from NBO calculations (kcal⋅mol−1) for the difluorinated pyrrolidines in the gas phase.
| isomer | ΔEfull | ΔELewis | ΔEnon-Lewis | nN→σ*CF | σCH→σ*CFa |
| 1 | 3.27 | 31.68 | −28.41 | 23.71 | 3.81 |
| 2 | 1.38 | 28.39 | −27.01 | 26.97 | 3.82 |
| 3 | 1.91 | 27.09 | −25.18 | 22.90 | 4.61 |
| 4 | 7.69 | 30.35 | −22.66 | 17.53 | 4.36 |
| 9 | 13.09 | 16.87 | −3.79 | 0.00 | 8.95 |
| 10 | 9.63 | 9.63 | 0.00 | 0.00 | 5.83 |
| 12 | 13.45 | 20.12 | −6.67 | 1.51 | 6.37 |
| 17 | 1.00 | 23.20 | −22.21 | 21.97 | 7.89 |
| 18 | 2.07 | 21.97 | −19.90 | 17.31 | 8.37 |
| 19 | 0.00 | 22.71 | −22.71 | 22.43 | 8.02 |
aSum of antiperiplanar σCH→σ*CF interactions.
Figure 6: σCH→σ*CF fluorine gauche interaction, which also occurred in 19, and anomeric interaction in isomer 19. The nN→σ*CF electron delocalization stabilized 19 by 22.43 kcal⋅mol−1.
Figure 6: σCH→σ*CF fluorine gauche interaction, which also occurred in 19, and anomeric interaction in isomer ...
Conclusion
Quantum-chemical calculations were conducted at the B3LYP-GD3BJ/6-311++G(d,p) level to assess isodesmic relationships for the most stable conformations of all isomers of 1,2- and 1,3- difluorinated pyrrolidines. This level of theory was chosen for its superior performance compared to other methodologies, as demonstrated through comparisons of the method with structural data on the 3-fluoropyrrolidinium cation and 3-fluoropyrrolidine. The conformational space of 2,3-, 2,4-, and 3,4-difluoropyrrolidines is notably dictated, both in the gas phase and implicit polar solution, by the N to C–F bond anomeric effect. Additionally, albeit less significant, electron delocalization from the C–H bonding orbital to the C–F antibonding orbital plays a crucial role in lowering the energy of isomers 17 and 19 relative to 1, 2, and 3. These insights deepen our understanding of the energetic principles governing molecular structures and provide valuable guidance in designing selectively fluorinated stereoisomers to influence preferred conformations when designing functional molecules.
Experimental
Computational details
The benchmark study was conducted for 3-fluoropyrrolidine and 3-fluoropyrrolidinium cation to determine the optimal theoretical level for further investigations involving 2,3-, 2,4-, and 3,4-difluoropyrrolidines, compared to the CCSD/DGTZVP level [14,15]. The evaluated levels encompassed the B3LYP-GD3BJ [16-18], ωB97XD [19], and PBEPBE [20] functionals, along with the 6-311++G(d,p) [21] and DGTZVP [15] basis sets. Following the identification of B3LYP-GD3BJ/6-311++G(d,p) as the most reliable method, it was employed to optimize the geometry and compute frequencies (to derive Gibbs free energy) for the difluorinated pyrrolidines. These computations were conducted in both the gas phase and employing an implicit DMSO solvent using SMD [22]. Subsequently, a NBO [23] analysis was performed for the gas-phase-optimized geometry at the same level of theory, utilizing the DEL (NOSTAR) keyword to discern Lewis- and non-Lewis-type contributions to the total electronic energy, alongside individual electronic delocalization interactions. The calculations were all performed using the Gaussian 16 package of software [24].
Supporting Information
| Supporting Information File 1: Standard orientations for the difluorinated pyrrolidines in the gas phase and DMSO. | ||
| Format: PDF | Size: 556.3 KB | Download |
Funding
The authors are grateful to Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES, funding code 001), Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq, grant number 306830/2021-3), and Fundação de Amparo à Pesquisa do Estado de Minas Gerais (FAPEMIG) for the financial support of this research.
Data Availability Statement
All data that supports the findings of this study is available in the published article and/or the supporting information to this article.
References
-
O’Hagan, D. J. Org. Chem. 2012, 77, 3689–3699. doi:10.1021/jo300044q
Return to citation in text: [1] -
Gakh, A. N. Monofluorinated Heterocycles. In Halogenated Heterocycles: Synthesis, Application and Environment; Iskra, J., Ed.; Springer: Heidelberg, Germany, 2012; pp 33–63. doi:10.1007/7081_2011_58
Return to citation in text: [1] -
Buissonneaud, D. Y.; van Mourik, T.; O'Hagan, D. Tetrahedron 2010, 66, 2196–2202. doi:10.1016/j.tet.2010.01.049
Return to citation in text: [1] -
Silla, J. M.; Silva, W. G. D. P.; Cormanich, R. A.; Rittner, R.; Tormena, C. F.; Freitas, M. P. J. Phys. Chem. A 2014, 118, 503–507. doi:10.1021/jp410458w
Return to citation in text: [1] [2] -
Gooseman, N. E. J.; O'Hagan, D.; Peach, M. J. G.; Slawin, A. M. Z.; Tozer, D. J.; Young, R. J. Angew. Chem., Int. Ed. 2007, 46, 5904–5908. doi:10.1002/anie.200700714
Return to citation in text: [1] -
Sun, A.; Lankin, D. C.; Hardcastle, K.; Snyder, J. P. Chem. – Eur. J. 2005, 11, 1579–1591. doi:10.1002/chem.200400835
Return to citation in text: [1] -
Lesarri, A.; Cocinero, E. J.; López, J. C.; Alonso, J. L. J. Am. Chem. Soc. 2005, 127, 2572–2579. doi:10.1021/ja045955m
Return to citation in text: [1] -
Freitas, M. P.; Rittner, R.; Tormena, C. F.; Abraham, R. J. Spectrochim. Acta, Part A 2005, 61, 1771–1776. doi:10.1016/j.saa.2004.07.007
Return to citation in text: [1] -
Martins, F. A.; Silla, J. M.; Freitas, M. P. Carbohydr. Res. 2017, 451, 29–35. doi:10.1016/j.carres.2017.09.007
Return to citation in text: [1] -
Hofman, G.-J.; Ottoy, E.; Light, M. E.; Kieffer, B.; Kuprov, I.; Martins, J. C.; Sinnaeve, D.; Linclau, B. Chem. Commun. 2018, 54, 5118–5121. doi:10.1039/c8cc01493k
Return to citation in text: [1] [2] -
Gao, J.-X.; Zhang, W.-Y.; Wu, Z.-G.; Zheng, Y.-X.; Fu, D.-W. J. Am. Chem. Soc. 2020, 142, 4756–4761. doi:10.1021/jacs.9b13291
Return to citation in text: [1] -
Roy, K.; Das, R. N.; Ambure, P.; Aher, R. B. Chemom. Intell. Lab. Syst. 2016, 152, 18–33. doi:10.1016/j.chemolab.2016.01.008
Return to citation in text: [1] -
Goodman, L.; Gu, H.; Pophristic, V. J. Phys. Chem. A 2005, 109, 1223–1229. doi:10.1021/jp046290d
Return to citation in text: [1] -
Cížek, J. On the Use of the Cluster Expansion and the Technique of Diagrams in Calculations of Correlation Effects in Atoms and Molecules. In Advances in Chemical Physics; LeFebvre, R.; Moser, C., Eds.; John Wiley & Sons: New York, NY, USA, 1969; Vol. 14, pp 35–89. doi:10.1002/9780470143599.ch2
Return to citation in text: [1] -
Godbout, N.; Salahub, D. R.; Andzelm, J.; Wimmer, E. Can. J. Chem. 1992, 70, 560–571. doi:10.1139/v92-079
Return to citation in text: [1] [2] -
Becke, A. D. Phys. Rev. A 1988, 38, 3098–3100. doi:10.1103/physreva.38.3098
Return to citation in text: [1] -
Lee, C.; Yang, W.; Parr, R. G. Phys. Rev. B 1988, 37, 785–789. doi:10.1103/physrevb.37.785
Return to citation in text: [1] -
Grimme, S.; Ehrlich, S.; Goerigk, L. J. Comput. Chem. 2011, 32, 1456–1465. doi:10.1002/jcc.21759
Return to citation in text: [1] -
Chai, J.-D.; Head-Gordon, M. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. doi:10.1039/b810189b
Return to citation in text: [1] -
Adamo, C.; Barone, V. J. Chem. Phys. 1999, 110, 6158–6170. doi:10.1063/1.478522
Return to citation in text: [1] -
McLean, A. D.; Chandler, G. S. J. Chem. Phys. 1980, 72, 5639–5648. doi:10.1063/1.438980
Return to citation in text: [1] -
Marenich, A. V.; Cramer, C. J.; Truhlar, D. G. J. Phys. Chem. B 2009, 113, 6378–6396. doi:10.1021/jp810292n
Return to citation in text: [1] -
NBO 7.0; Theoretical Chemistry Institute, University of Wisconsin–Madison: Madison, WI, USA, 2018.
Return to citation in text: [1] -
Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, 2016.
Return to citation in text: [1]
| 15. | Godbout, N.; Salahub, D. R.; Andzelm, J.; Wimmer, E. Can. J. Chem. 1992, 70, 560–571. doi:10.1139/v92-079 |
| 20. | Adamo, C.; Barone, V. J. Chem. Phys. 1999, 110, 6158–6170. doi:10.1063/1.478522 |
| 21. | McLean, A. D.; Chandler, G. S. J. Chem. Phys. 1980, 72, 5639–5648. doi:10.1063/1.438980 |
| 5. | Gooseman, N. E. J.; O'Hagan, D.; Peach, M. J. G.; Slawin, A. M. Z.; Tozer, D. J.; Young, R. J. Angew. Chem., Int. Ed. 2007, 46, 5904–5908. doi:10.1002/anie.200700714 |
| 16. | Becke, A. D. Phys. Rev. A 1988, 38, 3098–3100. doi:10.1103/physreva.38.3098 |
| 17. | Lee, C.; Yang, W.; Parr, R. G. Phys. Rev. B 1988, 37, 785–789. doi:10.1103/physrevb.37.785 |
| 18. | Grimme, S.; Ehrlich, S.; Goerigk, L. J. Comput. Chem. 2011, 32, 1456–1465. doi:10.1002/jcc.21759 |
| 4. | Silla, J. M.; Silva, W. G. D. P.; Cormanich, R. A.; Rittner, R.; Tormena, C. F.; Freitas, M. P. J. Phys. Chem. A 2014, 118, 503–507. doi:10.1021/jp410458w |
| 19. | Chai, J.-D.; Head-Gordon, M. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. doi:10.1039/b810189b |
| 3. | Buissonneaud, D. Y.; van Mourik, T.; O'Hagan, D. Tetrahedron 2010, 66, 2196–2202. doi:10.1016/j.tet.2010.01.049 |
| 10. | Hofman, G.-J.; Ottoy, E.; Light, M. E.; Kieffer, B.; Kuprov, I.; Martins, J. C.; Sinnaeve, D.; Linclau, B. Chem. Commun. 2018, 54, 5118–5121. doi:10.1039/c8cc01493k |
| 13. | Goodman, L.; Gu, H.; Pophristic, V. J. Phys. Chem. A 2005, 109, 1223–1229. doi:10.1021/jp046290d |
| 2. | Gakh, A. N. Monofluorinated Heterocycles. In Halogenated Heterocycles: Synthesis, Application and Environment; Iskra, J., Ed.; Springer: Heidelberg, Germany, 2012; pp 33–63. doi:10.1007/7081_2011_58 |
| 14. | Cížek, J. On the Use of the Cluster Expansion and the Technique of Diagrams in Calculations of Correlation Effects in Atoms and Molecules. In Advances in Chemical Physics; LeFebvre, R.; Moser, C., Eds.; John Wiley & Sons: New York, NY, USA, 1969; Vol. 14, pp 35–89. doi:10.1002/9780470143599.ch2 |
| 15. | Godbout, N.; Salahub, D. R.; Andzelm, J.; Wimmer, E. Can. J. Chem. 1992, 70, 560–571. doi:10.1139/v92-079 |
| 8. | Freitas, M. P.; Rittner, R.; Tormena, C. F.; Abraham, R. J. Spectrochim. Acta, Part A 2005, 61, 1771–1776. doi:10.1016/j.saa.2004.07.007 |
| 9. | Martins, F. A.; Silla, J. M.; Freitas, M. P. Carbohydr. Res. 2017, 451, 29–35. doi:10.1016/j.carres.2017.09.007 |
| 11. | Gao, J.-X.; Zhang, W.-Y.; Wu, Z.-G.; Zheng, Y.-X.; Fu, D.-W. J. Am. Chem. Soc. 2020, 142, 4756–4761. doi:10.1021/jacs.9b13291 |
| 4. | Silla, J. M.; Silva, W. G. D. P.; Cormanich, R. A.; Rittner, R.; Tormena, C. F.; Freitas, M. P. J. Phys. Chem. A 2014, 118, 503–507. doi:10.1021/jp410458w |
| 12. | Roy, K.; Das, R. N.; Ambure, P.; Aher, R. B. Chemom. Intell. Lab. Syst. 2016, 152, 18–33. doi:10.1016/j.chemolab.2016.01.008 |
| 7. | Lesarri, A.; Cocinero, E. J.; López, J. C.; Alonso, J. L. J. Am. Chem. Soc. 2005, 127, 2572–2579. doi:10.1021/ja045955m |
| 22. | Marenich, A. V.; Cramer, C. J.; Truhlar, D. G. J. Phys. Chem. B 2009, 113, 6378–6396. doi:10.1021/jp810292n |
| 6. | Sun, A.; Lankin, D. C.; Hardcastle, K.; Snyder, J. P. Chem. – Eur. J. 2005, 11, 1579–1591. doi:10.1002/chem.200400835 |
| 10. | Hofman, G.-J.; Ottoy, E.; Light, M. E.; Kieffer, B.; Kuprov, I.; Martins, J. C.; Sinnaeve, D.; Linclau, B. Chem. Commun. 2018, 54, 5118–5121. doi:10.1039/c8cc01493k |
| 23. | NBO 7.0; Theoretical Chemistry Institute, University of Wisconsin–Madison: Madison, WI, USA, 2018. |
© 2024 Silva et al.; licensee Beilstein-Institut.
This is an open access article licensed under the terms of the Beilstein-Institut Open Access License Agreement (https://www.beilstein-journals.org/bjoc/terms), which is identical to the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0). The reuse of material under this license requires that the author(s), source and license are credited. Third-party material in this article could be subject to other licenses (typically indicated in the credit line), and in this case, users are required to obtain permission from the license holder to reuse the material.