Abstract
In contrast to theoretical expectations, the photolysis of 2,4,6-triazido-3-chloro-5-fluoropyridine in argon at 5 K gives rise to EPR peaks of just two triplet mononitrenes, two quintet dinitrenes, and a septet trinitrene. EPR spectral simulations in combination with DFT calculations show that observable nitrenes can be assigned to triplet 2,4-diazido-3-chloro-5-fluoropyridyl-6-nitrene (DT = 1.026 cm−1, ET = 0), triplet 2,6-diazido-3-chloro-5-fluoropyridyl-4-nitrene (DT = 1.122 cm−1, ET = 0.0018 cm−1), quintet 4-azido-3-chloro-5-fluoropyridyl-2,6-dinitrene (DQ = 0.215 cm−1, EQ = 0.0545 cm−1), quintet 2-azido-3-chloro-5-fluoropyridyl-4,6-dinitrene (DQ = 0.209 cm−1, EQ = 0.039 cm−1) and septet 3-chloro-5-fluoropyridyl-2,4,6-trinitrene (DS = −0.1021 cm−1, ES = −0.0034 cm−1). Preferential photodissociation of the azido groups located in ortho-positions to the fluorine atom of pyridines is associated with strong π-conjugation of these groups with the pyridine ring. On photoexcitation, such azido groups are more efficiently involved in reorganization of the molecular electronic system and more easily adopt geometries of the locally excited predissociation states.
Graphical Abstract
Introduction
High-spin nitrenes are highly reactive intermediates formed during photolysis or thermolysis of aromatic polyazides. Both these processes are widely used in modern science and technology [1-6]. When aromatic polyazides contain nonequivalent azido groups, these groups can undergo selective photolysis, providing important information about the selective cleavage of chemical bonds in organic molecules with light. The direction and selectivity of such processes can be monitored with EPR spectroscopy allowing the reliable identification of isomeric high-spin nitrenes [7-10]. Thus, previous EPR studies have shown that irradiation of triazide 1a with light at λ = 313 nm selectively gave quintet dinitrene 4a as the major intermediate product (Scheme 1) [7,8]. Most recently, a similar selectivity was observed during the photolysis of triazide 1b where quintet dinitrene 4b was the major intermediate product (Scheme 1) [9]. By contrast, the photolysis of triazide 7 occurs selectively on the azido group located on the γ-phenyl ring, yielding dinitrene 9 as a single quintet intermediate (Scheme 1) [10]. All these photochemical studies became possible owing to extensive EPR investigations of various high-spin nitrenes in the past two decades [11-31]. Nowadays, the EPR spectral identification of high-spin nitrenes is based on comparison of their zero-field splitting (ZFS) parameters derived from experimental EPR spectra and calculated by quantum chemistry methods. The most accurate theoretical estimations are obtained at the PBE/DZ level of theory, which overestimates the experimental ZFS values of nitrenes by only about 10% [32]. This accuracy of calculations is sufficient for reliable identification of isomeric dinitrenes 4a–c and 5a–c formed during the photolysis of triazides 1a–c (Scheme 1). Although these dinitrenes show nearly the same DQ values (≈0.21 cm−1), the EQ values of 4a–c and 5a–c differ significantly (EQ4 ≈ 0.055 cm−1, EQ5 ≈ 0.040 cm−1), thus allowing one to unambiguously discriminate such isomers [29-31].
Scheme 1: Examples of selective photolysis of the azido groups.
Scheme 1: Examples of selective photolysis of the azido groups.
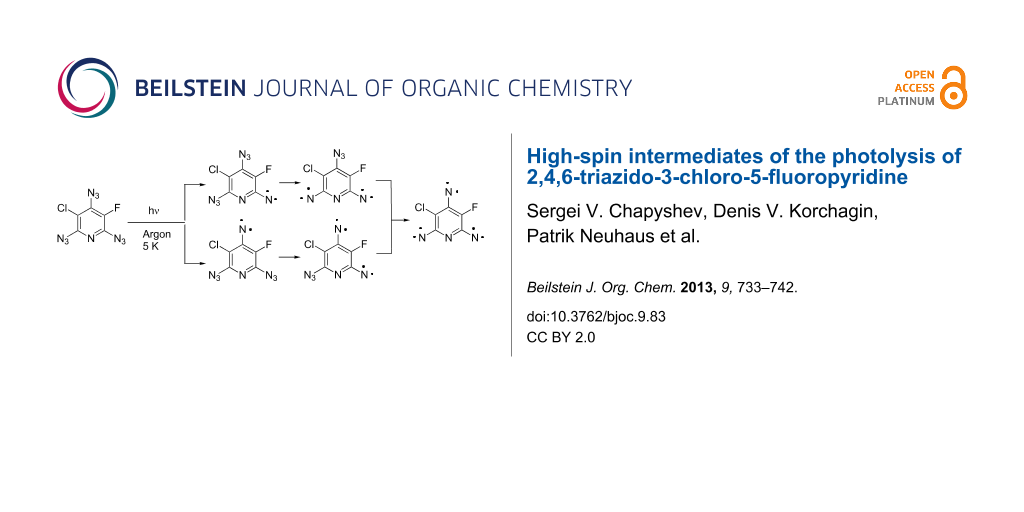
A new level of complexity is the EPR identification of high-spin intermediates formed during the photolysis of asymmetric triazides such as 11 (Scheme 2). Theoretically, the photolysis of triazide 11 may give three triplet nitrenes 12–14, three quintet dinitrenes 15–17, and septet trinitrene 18. So far, no attempt was undertaken to discriminate such structurally alike isomers as quintet dinitrenes 16 and 17.
Scheme 2: Possible photoproducts of triazide 11.
Scheme 2: Possible photoproducts of triazide 11.
In the present work, we report on matrix isolation and EPR studies of high-spin intermediates formed during the photolysis of asymmetric triazide 11, providing the first information about selective photochemical decomposition of three nonequivalent azido groups in monocyclic aromatic compounds.
Results and Discussion
Brief UV irradiation (2 min, λ = 260–320 nm) of triazide 11 in the argon matrix leads to the appearance of just two strong EPR signals of triplet nitrenes at 6985 and 7217 G as well as weak Y2-transitions of quintet dinitrenes at 3077 and 3337 G. Upon more extended irradiation, new signals in the 30–7000 G region appear due to gradual accumulation of high-spin nitrenes. The intensities of these signals reached their maximum values after 45 min of irradiation and then gradually decayed upon further irradiation. The EPR spectrum recorded after 45 min of irradiation is shown in Figure 1b.
![[1860-5397-9-83-1]](/bjoc/content/figures/1860-5397-9-83-1.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 1: EPR spectra: (a) simulated spectrum for a mixture of five nitrenes with (i) S = 1, g = 2.003, DT = 1.026 cm−1 and ET = 0; (ii) S = 1, g = 2.003, DT = 1.122 cm−1 and ET = 0.0018 cm−1; (iii) S = 2, g = 2.003, DQ = 0.209 cm−1, EQ = 0.039 cm−1; (iv) S = 2, g = 2.003, DQ = 0.215 cm−1, EQ = 0.0545 cm−1; (v) S = 3, g = 2.003, DS = –0.1021 cm−1, ES = –0.0034 cm−1 in a 14:12:20:5:1 ratio; (b) experimental spectrum after 45 min of UV irradiation of triazide 11. Microwave frequency ν0 = 9.605832 GHz.
Figure 1: EPR spectra: (a) simulated spectrum for a mixture of five nitrenes with (i) S = 1, g = 2.003, DT = ...
The EPR spectral simulations show that the products of the reaction are two triplet nitrenes with DT = 1.026 cm−1, ET = 0 cm−1 and DT = 1.122 cm−1, ET = 0.0018 cm−1, two quintet dinitrenes with DQ = 0.209 cm−1, EQ = 0.039 cm−1 and DQ = 0.215 cm−1, EQ = 0.0545 cm−1, and a septet trinitrene with DS = −0.1021 cm−1, ES = −0.0034 cm−1 in a 14:12:20:5:1 ratio (Figure 1a). Surprisingly, the ZFS parameters of quintet and septet nitrenes formed in the reaction were very close to the magnetic parameters of previously studied quintet dinitrenes 4c (DQ = 0.210 cm−1, EQ = 0.039 cm−1) and 5c (DQ = 0.209 cm−1, EQ = 0.0542 cm−1) and septet trinitrene 6c (DS = −0.1011 cm−1, ES = −0.0043 cm−1) [31]. The EPR spectra of such nitrenes, including the complete assignment of all transitions, have been reported previously [29-31]. Quintet and septet nitrenes formed during the photolysis of triazide 11 display very similar EPR spectra.
The septet product formed in the reaction can be safely assigned to trinitrene 18 since only this trinitrene has a septet spin state. According to EPR spectral simulations (Figure 1a), this trinitrene is formed in ca. 2% yield. Due to different substituents in positions 3 and 5 of the pyridine ring, trinitrene 18 has different angles Θ1, Θ2, Θ3 between the nitrene C–N bonds and different Mulliken spin populations on the nitrene units (Table 1). Theoretically, such asymmetric trinitrenes should show rather large ES values [30]. Nevertheless, the ES value of trinitrene 18 is even smaller than that of C2v symmetric trinitrene 6c [31]. DFT calculations show that trinitrene 18, on comparison with C2v symmetric trinitrenes 6a-c, has slightly different orientations of the principal magnetic axes due to the presence of only one heavy chlorine atom. Thus, the principal axes DXXSS and DXXTot of C2v symmetric trinitrene 6a were directed along the line connecting the nitrene units in positions 2 and 6 of the pyridine ring and were parallel to the DZZSO axis of the spin–orbit tensor DSO connecting two heavy chlorine atoms in positions 3 and 5 of the pyridine ring [30]. In the case of trinitrene 18, the DZZSO axis of the spin-orbit tensor DSO almost coincides with the C(3)–Cl bond (Figure 2). As a result, the principal axis DXXTot in trinitrene 18 is turned away from the line connecting the α-nitrene units by about 4°.
Table 1: Mulliken spin populations ρN on the nitrene units and dipolar angles Θ between the nitrene C–N/C–N bonds in high-spin nitrenes 15–18.
| Parameter | Nitrene | |||
|---|---|---|---|---|
| 15 | 16 | 17 | 18 | |
| ρN |
1.63 (2N)
1.62 (6N) |
1.55 (4N)
1.53 (6N) |
1.53 (2N)
1.55 (4N) |
1.62 (2N)
1.54 (4N) 1.63 (6N) |
| Θ [°] | 115.7 (2N/6N) | 121.6 (4N/6N) | 125.4 (2N/4N) |
124.8 (2N/4N)
121.2 (4N/6N) 113.9 (2N/6N) |
Figure 2: UB3LYP/6-311G*+BLYP/EPRII calculated orientations of the tensors DSS and DSO in nitrenes 15–18. The tensors DSS and DTot have the same orientations.
Figure 2: UB3LYP/6-311G*+BLYP/EPRII calculated orientations of the tensors DSS and DSO in nitrenes 15–18. The...
Previous studies of nitrenes 6a–c have shown that the most accurate theoretical evaluations of DS and ES by the DFT approach were obtained by using the PBE and BLYP functionals in combination with the DZ or EPRII basis sets [32]. Extensive DFT calculations performed in the present work show that the best agreement between the experiment and theory is observed at the BLYP/EPRII level of theory, overestimating the experimental DS and ES values of trinitrene 18 by only 6% (Table 2). The breakdown of DS and ES into DSS, DSO, ESS, and ESO reveals that the BLYP/EPRII calculations are especially good in estimations of the spin–orbit coupling contributions ESO to the small parameters ES of septet trinitrenes (Table 3).
Table 2: DFT calculated and experimental parameters D/E in cm−1 of nitrenes 15–18.
| Method | D/E of 15 | D/E of 16 | D/E of 17 | D/E of 18 |
|---|---|---|---|---|
| PBE/TZV | — | — | — | −0.1122/−0.0044 |
| PBE/6-311+G* | — | — | — | −0.1104/−0.0044 |
| BLYP/DZ | 0.2249/0.0610 | 0.2302/0.0398 | 0.2304/0.0422 | −0.1116/−0.0045 |
| PBE/DZ | 0.2226/0.0609 | 0.2279/0.0400 | 0.2303/0.0416 | −0.1108/−0.0046 |
| PBE/EPRII | 0.2261/0.0574 | 0.2265/0.0369 | 0.2289/0.0387 | −0.1089/−0.0042 |
| BLYP/EPRII | 0.2259/0.0572 | 0.2270/0.0366 | 0.2269/0.0394 | −0.1090/−0.0036 |
| Experiment | 0.2150/0.0545 | 0.2090/0.0390 | — | −0.1021/−0.0034 |
Table 3: DFT calculated parameters DSS/ESS and DSO/ESO in cm−1 of nitrenes 15–18.
| Nitrene | Method | DSS/ESS | DSO/ESO |
|---|---|---|---|
| 15 | PBE/DZ | 0.201/0.059 | 0.021/0.002 |
| PBE/EPRII | 0.204/0.055 | 0.022/0.002 | |
| BLYP/EPRII | 0.202/0.055 | 0.024/0.002 | |
| 16 | PBE/DZ | 0.212/0.040 | 0.016/0.001 |
| PBE/EPRII | 0.211/0.036 | 0.016/0.001 | |
| BLYP/EPRII | 0.209/0.035 | 0.018/0.001 | |
| 17 | PBE/DZ | 0.229/0.034 | 0.002/0.007 |
| PBE/EPRII | 0.227/0.031 | 0.002/0.007 | |
| BLYP/EPRII | 0.226/0.030 | 0.002/0.007 | |
| 18 | PBE/DZ | −0.1031/−0.0078 | −0.008/0.003 |
| PBE/EPRII | −0.1007/−0.0074 | −0.008/0.003 | |
| BLYP/EPRII | −0.0996/−0.0075 | −0.009/0.004 | |
By analogy with previous studies of dinitrenes 5a–c [29-31], the quintet molecule with DQ = 0.215 cm−1 and EQ = 0.0545 cm−1 can safely be assigned to dinitrene 15 with Θ = 115.7°. Thus, for instance, quintet dinitrene 5a showed DQ = 0.202 cm−1 and EQ = 0.0554 cm−1 [30], and its difluoro-derivative 5b displayed DQ = 0.213 cm−1 and EQ = 0.0556 cm−1 [29]. The most accurate theoretical estimations of the magnetic parameters in dinitrene 5a–c were obtained by using the PBE/DZ calculations [32]. Such calculations are also the most accurate for estimations of DQ in dinitrene 15 (Table 2). The theoretical value of DQ = 0.2226 cm−1 obtained from the PBE/DZ calculations overestimates the experimental DQ value in dinitrene 15 by just 3.5%. On the other hand, as in the case with trinitrene 18, the BLYP/EPRII calculations predict the most realistic value of EQ = 0.0572 cm−1 in dinitrene 15 (Table 2). According to EPR spectral simulations, dinitrene 15 is formed in the photolysis of triazide 11 in only ca. 10% yield.
The major quintet product of the reaction is the dinitrene with DQ = 0.209 cm−1 and EQ = 0.039 cm−1 (38%). This dinitrene can be assigned either to dinitrene 16 or to dinitrene 17. Previous EPR studies have shown that quintet dinitrenes with Θ = 121 ± 1° displayed EQ = 0.04 ± 0.001 cm−1, and dinitrenes with Θ = 125 ± 1° showed EQ = 0.035 ± 0.001 cm−1 [21,29-31]. According to DFT calculations, the dipolar angles Θ in dinitrenes 16 and 17 are equal to 121.6° and 125.4°, respectively (Table 1). These data suggest that the dinitrene with EQ = 0.039 cm−1 can safely be assigned to dinitrene 16. The most realistic theoretical estimation of EQ in dinitrene 16 is obtained from PBE/DZ calculations of the spin–spin interaction parameter EQSS (Table 3). This fact indicates that the contribution of the spin–orbit interactions to the total parameter EQ of dinitrene 16 is quite small, as is typical for most of quintet dinitrenes [32].
Although we do not observe diagnostic signals of dinitrene 17 in the experimental EPR spectrum, this dinitrene may be a minor product of the photolysis of triazide 11. Extensive EPR spectral simulations show that five other quintet molecules with EQ/DQ = 0.038/0.213, 0.037/0.217, 0.036/0.221, 0.035/0.225 and 0.034/0.229 also display intense Y2 transitions at 3077 G beside dinitrene 16 with EQ/DQ = 0.039/0.209. In EPR spectra of individual molecules, these six quintet species are easily identified owing to different positions of their Z1, X1, X2, Z2, A1 and A2 transitions (See Supporting Information File 1). However, when the mixture of dinitrenes 16 and 17 is formed, isomer 17 becomes detectable in EPR spectra only at relatively high concentrations (>5%). Thus, for instance, in EPR spectra of two quintet molecules with EQ/DQ = 0.039/0.209 and 0.038/0.213, the minor component with EQ/DQ = 0.038/0.213 becomes visible when its ratio to the major component exceeds 1:6 (14%). Based on these data, we do not exclude that dinitrene 17 with EQ/DQ ≈ 0.036/0.221 may be formed in ca. 5% yield along with dinitrene 16 (≈33%) during the photolysis of triazide 11.
Theoretically, several triplet mononitrenes can be formed during the photolysis of triazide 11 (Figure 3). As a rule, triplet pyridyl-2-nitrenes show DT = 1.03 ± 0.02 cm−1 and ET ≈ 0 cm−1, while triplet pyridyl-4-nitrenes show DT = 1.13 ± 0.02 cm−1 and ET ≈ 0 cm−1 [29-31]. When chlorine atoms are set in ortho-positions to the nitrene center, such triplet pyridylnitrenes show ET > 0.003 cm−1 [30]. Since one of triplet mononitrenes obtained in the present work shows DT = 1.026 cm−1 and ET = 0 cm−1, this nitrene can safely be assigned to 12 (Scheme 2). Another triplet mononitrene shows a DT = 1.122 cm−1 typical for pyridyl-4-nitrenes and a small parameter ET = 0.0018 cm−1 that is characteristic for triplet nitrenes with one chlorine atom in an ortho-position to the nitrene center. This mononitrene can safely be assigned to 13. According to EPR spectral simulations, triplet nitrenes 12 and 13 are formed in 27 and 23% yield, respectively. DFT calculations of the parameters DTSS agree well with the experiment, overestimating the DT parameters of nitrenes 12 and 13 by just 2 and 3%, respectively (Figure 3). Unfortunately, as in the case of many other triplet mononitrenes [32], such calculations are too crude for estimations of the parameters ET, predicting ET = 0.006 ± 0.001 cm−1 for all isomers of 12–14.
Figure 3: Mulliken spin populations on the nitrene units and parameters DTSS in cm−1 of triplet nitrenes 12–14 at the PBE/DZ level of theory.
Figure 3: Mulliken spin populations on the nitrene units and parameters DTSS in cm−1 of triplet nitrenes 12–14...
Recent EPR studies have shown that the best EPR spectral simulations for high-spin nitrenes were obtained only when an additional line-broadening parameter Γ(E) was used in the spin-Hamiltonian calculations [24]. The necessity of the use of this parameter in calculations is due to the presence in matrices of numerous conformational isomers of the starting azides. Upon UV irradiation, these conformers decompose to high-spin nitrenes that slightly differ each from other in the angles N–C–C and Θ and the parameters E. The formation of such high-spin nitrenes affects significantly the line-width and intensity of some lines in the experimental EPR spectra. Similar effects were also observed in EPR spectra of nitrenes 15–18. In order to adequately reproduce the experimental EPR spectrum from Figure 1b, the line-broadening parameters Γ(E) = 75 MHz for dinitrenes 15 and 16 and Γ(E) = 40 MHz for trinitrene 18 were used in the spectral simulations. According to these values of Γ(E), the variations in the angles Θ for dinitrenes 15/16 and trinitrene 18 do not exceed 0.7° and 0.4°, respectively. Despite these very small variations in the angles Θ, all our attempts to theoretically reproduce the experimental EPR spectrum from Figure 1b without the use of the line-broadening parameters Γ(E) were unsuccessful. EPR spectra of nitrenes 15, 16 and 18 simulated for Γ(E) = 0, 40 and 75 MHz are presented in Supporting Information File 1.
The results obtained show that almost all triplet and quintet nitrenes detected in the present study arise from the photolysis of the azido groups located in ortho-positions to the fluorine atom of pyridines. On comparison with the chlorine, the fluorine is a much more electron-negative and less bulky atom. Both of these factors favor strong π– conjugation of the ortho-azido groups with the pyridine ring. On photoexcitation, such azido groups should be more efficiently involved in reorganization of the molecular electronic system and more easily adopt geometries of the locally excited predissociation states [33,34]. DFT calculations show that namely azido groups located in positions 4 and 6 of triazide 11 have high localization of the lowest unoccupied molecular orbital (LUMO) density (see below in Figure 4). Similar localization of the LUMO density has previously been calculated for the azido group set on the γ-phenyl ring of triazide 7, which underwent selective photolysis to form triplet nitrene 8 (Scheme 1) [10]. All these data indicate that of the three azido groups of triazide 11 the azido groups in ortho-positions to the fluorine atom should be the most photoactive.
The photodissociation of the azido groups in triazide 11 can be modeled by computational methods [8,34]. Thus, for instance, the geometry optimizations of the most stable rotamers 11a and 11b in their lowest singlet excited states by using CIS/PM3 or CIS/6-311+G* calculations yield structures 11a-S1* and 11b-S1*, in which the azido groups in ortho-positions to the fluorine atom are locally excited (Scheme 3). These calculations confirm that the local excitation of such groups requires lower activation energies [8,34]. According to theory [34-36], the local excitation of the azido group during the photoexcitation results in considerable bending of the N=N=N fragment from about 171° to about 117° and appearance of the σ-type antibonding interactions in the N–N2 bond. Figure 4 illustrates these effects for the structure 11a-S1*.
Scheme 3: Initial stages of the photolysis of triazide 11.
Scheme 3: Initial stages of the photolysis of triazide 11.
![[1860-5397-9-83-4]](/bjoc/content/figures/1860-5397-9-83-4.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 4: UB3LYP/6-311+G* orbital density in the LUMO of triazide 11 and CIS/6-311+G* orbital density in the highest singly occupied orbital of excited state 11a-S1*.
Figure 4: UB3LYP/6-311+G* orbital density in the LUMO of triazide 11 and CIS/6-311+G* orbital density in the ...
Thus, the first stage of the photolysis of triazide 11 in argon matrices involves the photochemical generation of excited states 11a-S1* and 11b-S1*, which then undergo dissociation of the locally excited azido groups to form triplet nitrenes 12 and 13 (Scheme 3). On the second stage, triplet nitrenes 12 and 13 are excited to triplet states 12a-T1*, 12b-T1* and 13a-T1* which then dissociate to quintet dinitrenes 15 and 16. The latter is formed as the major product owing to efficient excitation of the azido groups located in ortho-positions to the fluorine atom of nitrenes 12 and 13. The photoexcitation of the azido group in position 2 of nitrene 12 is a less efficient process leading to the formation of dinitrene 15 in just about 10% yield. The photoexcitation of the azido group in position 2 of nitrene 13 is a still much less efficient process. Quintet dinitrene 17 either is not formed at all or its yield is very low (<6%). Finally, the photodecomposition of the remaining azido groups in dinitrenes 15 and 16 gives septet trinitrene 18 in just about 2% yield. The low yield of trinitrene 18 may be associated with low efficiency of the azido group excitation in quintet dinitrene 16. One also cannot exclude that the photoexcitation of quintet azidonitrenes into predissociation states is a much less efficient process in comparison with the photoexcitation of singlet azides. In contrast to singlet azides, quintet azidonitrenes already have four singly occupied orbitals, and photoexcitation of these species may lead to excited states in which the azido groups are not locally excited.
Conclusion
In contrast to theoretical expectations, photodissociation of triazide 11 with light at λ = 260–320 nm occurs selectively on the azido groups located in positions 4 and 6 of the pyridine ring to give triplet mononitrenes 12 and 13 as the primary photoproducts. On further irradiation, quintet dinitrenes 15 and 16 and septet trinitrene 18 are formed. The maximum yield of the latter is about just 2%. Preferential photodissociation of the azido groups located in ortho-positions to the fluorine atom of pyridines is associated with strong π-conjugation of these groups with the pyridine ring. On photoexcitation, such azido groups are more efficiently involved in reorganization of the molecular electronic system and more easily adopt geometries of the locally excited predissociation states. Despite the lack of symmetry, trinitrene 18 shows a small parameter of ES = −0.0034 cm−1 due to a large positive value of the spin-orbit coupling parameter ES SO (≈0.005 cm−1). In overall, the ZFS parameters of 18 are very close to the ZFS parameters of previously studied C2v symmetric septet pyridyl-2,4,6-trinitrenes. The most accurate theoretical predictions of the ZFS parameters of 18 are obtained at the BLYP/EPRII level of theory. At the same time, modern DFT calculations are still too crude to be used for reliable EPR spectral identification of such structurally alike quintet isomers as dinitrenes 16 and 17. Such quintet isomers are better discriminated based on analysis of their dipolar angles Θ. Among theoretical approaches, the most accurate estimations of the ZFS parameters of dinitrene 16 are obtained from PBE/DZ calculations of its parameters DSSS and ESSS. The study also demonstrates that successful EPR spectral simulations for nitrenes 15, 16 and 18 are possible only if additional line-broadening parameters Γ(E) of 40–75 MHz along with appropriate values of g, S, D, E and ν0 are used in the spin-Hamiltonian calculations.
Experimental
Triazide 11 was synthesized according to the literature procedure [37]. X-band EPR spectra were recorded with a Bruker-Elexsys E500 EPR spectrometer with an ER077R magnet (75 mm gap between pole faces), an ER047 XG-T microwave bridge, and an ER4102ST resonator with a TE102 cavity. Solid argon matrices doped with triazide 11 were prepared by vacuum co-deposition of two separate molecular beams (Ar and triazide 11 vapor) on the tip of an oxygen-free high-conductivity copper rod (75 mm length, 3 mm diameter) cooled at 5 K. The vapor of 11 was produced by an oven heating the polycrystalline 11 to 60 °C. The matrix-isolated samples were irradiated with a high-pressure mercury lamp, by using a filter passing the light at λ = 260–320 nm, and spectra were recorded at various irradiation times.
The computer simulations of EPR spectra were performed by using the EasySpin program package (version 4.0.0) [38]. The simulations were performed by using matrix diagonalization methods for S = 1, 2 or 3 using the parameters ν0 = 9.605832 GHz and g = 2.0023 and line widths ΔH = 60 G for S = 1, and 30 G for S = 2 and S = 3.
The geometries of the molecules were optimized at the B3LYP/6-311G(d) level of theory with the Gaussian 03 program package [39]. The nature of the stationary points was assessed by means of vibrational frequency analysis. The spin-Hamiltonian parameters (g, D, E) and orientations of the D tensor were obtained from additional single-point calculations with the ORCA program package [40,41]. DFT calculations of the direct spin–spin (SS) coupling DSS and spin–orbit coupling (SO) DSO parts of the D tensors were performed by using the McWeeny–Mizuno and Pederson–Khanna approaches, respectively [42].
Supporting Information
Supporting Information features EPR spectral simulations for quintet dinitrenes 15–17 and septet trinitrene 18 as individual species and for the mixtures of quintet molecules with EQ/DQ = 0.039/0.209, 0.038/0.213 and 0.036/0.221 at different molar ratios as well as EPR spectral simulations for nitrenes 15, 16 and 18 at different values of the line-broadening parameter Γ(E).
| Supporting Information File 1: EPR spectral simulations. | ||
| Format: PDF | Size: 254.5 KB | Download |
References
-
Bräse, S.; Banert, K., Eds. Organic Azides: Synthesis and Applications; Wiley-VCH: Chichester, U.K., 2010.
Return to citation in text: [1] -
Scriven, F. F. V., Ed. Azides and Nitrenes, Reactivity and Utility; Academic Press: New York, USA, 1984.
Return to citation in text: [1] -
Bräse, S.; Gil, C.; Knepper, K.; Zimmermann, V. Angew. Chem., Int. Ed. 2005, 44, 5188–5240. doi:10.1002/anie.200400657
Return to citation in text: [1] -
Scriven, E. V. F.; Turnbull, K. Chem. Rev. 1988, 88, 297–368. doi:10.1021/cr00084a001
Return to citation in text: [1] -
Chapyshev, S. V. Synlett 2009, 1–8. doi:10.1055/s-0028-1087479
Return to citation in text: [1] -
Chapyshev, S. V. Russ. Chem. Bull. 2011, 60, 1274–1285. doi:10.1007/s11172-011-0195-7
Return to citation in text: [1] -
Chapyshev, S. V.; Walton, R.; Sanborn, J. A.; Lahti, P. M. J. Am. Chem. Soc. 2000, 122, 1580–1588. doi:10.1021/ja993131c
Return to citation in text: [1] [2] -
Chapyshev, S. V.; Walton, R.; Lahti, P. M. Mendeleev Commun. 2000, 10, 187–188. doi:10.1070/MC2000v010n05ABEH001308
Return to citation in text: [1] [2] [3] [4] -
Finke, C.; Grote, D.; Seidel, R. W.; Chapyshev, S. V.; Sander, W. J. Phys. Org. Chem. 2012, 25, 486–492. doi:10.1002/poc.1943
Return to citation in text: [1] [2] -
Chapyshev, S. V.; Korchagin, D. V.; Budyka, M. F.; Gavrishova, T. N.; Neuhaus, P.; Sander, W. ChemPhysChem 2012, 13, 2721–2728. doi:10.1002/cphc.201200200
Return to citation in text: [1] [2] [3] -
Nimura, S.; Yabe, A. In Magnetic Properties of Organic Materials; Lahti, P. M., Ed.; Marcel Dekker: New York, 1999; pp 127–145.
Return to citation in text: [1] -
Fukuzawa, T. A.; Sato, K.; Ichimura, A. S.; Kinoshita, T.; Takui, T.; Itoh, K.; Lahti, P. M. Mol. Cryst. Liq. Cryst. 1996, 278, 253–260. doi:10.1080/10587259608033683
Return to citation in text: [1] -
Kalgutkar, R. S.; Lahti, P. M. J. Am. Chem. Soc. 1997, 119, 4771–4772. doi:10.1021/ja963723k
Return to citation in text: [1] -
Chapyshev, S. V.; Walton, R.; Lahti, P. M. Mendeleev Commun. 2000, 10, 114–115. doi:10.1070/MC2000v010n03ABEH001281
Return to citation in text: [1] -
Miura, Y.; Oka, H.; Teki, Y. Bull. Chem. Soc. Jpn. 2001, 74, 385–386. doi:10.1246/bcsj.74.385
Return to citation in text: [1] -
Kalgutkar, R. S.; Lahti, P. M. Tetrahedron Lett. 2003, 44, 2625–2628. doi:10.1016/S0040-4039(03)00385-X
Return to citation in text: [1] -
Chapyshev, S. V.; Tomioka, H. Bull. Chem. Soc. Jpn. 2003, 76, 2075–2089. doi:10.1246/bcsj.76.2075
Return to citation in text: [1] -
Sato, T.; Narazaki, A.; Kawaguchi, Y.; Niino, H.; Bucher, G.; Grote, D.; Wolff, J. J.; Wenk, H. H.; Sander, W. J. Am. Chem. Soc. 2004, 126, 7846–7852. doi:10.1021/ja031794v
Return to citation in text: [1] -
Chapyshev, S. V.; Walton, R.; Serwinski, P. R.; Lahti, P. M. J. Phys. Chem. A 2004, 108, 6643–6649. doi:10.1021/jp048764e
Return to citation in text: [1] -
Chapyshev, S. V.; Lahti, P. M. J. Phys. Org. Chem. 2006, 19, 637–641. doi:10.1002/poc.1106
Return to citation in text: [1] -
Chapyshev, S. V. Russ. Chem. Bull. 2006, 55, 1126–1131. doi:10.1007/s11172-006-0388-7
Return to citation in text: [1] [2] -
Chapyshev, S. V. Russ. Chem. Bull. 2006, 55, 1593–1597. doi:10.1007/s11172-006-0459-9
Return to citation in text: [1] -
Misochko, E. Ya.; Akimov, A. V.; Chapyshev, S. V. J. Chem. Phys. 2008, 128, No. 124504. doi:10.1063/1.2840351
Return to citation in text: [1] -
Koto, T.; Sato, K.; Shiomi, D.; Toyota, K.; Itoh, K.; Wasserman, E.; Takui, T. J. Phys. Chem. A 2009, 113, 9521–9526. doi:10.1021/jp9042717
Return to citation in text: [1] [2] -
Chapyshev, S. V.; Misochko, E. Ya.; Akimov, A. V.; Dorokhov, V. G.; Neuhaus, P.; Grote, D.; Sander, W. J. Org. Chem. 2009, 74, 7238–7244. doi:10.1021/jo9010848
Return to citation in text: [1] -
Chapyshev, S. V. Russ. J. Phys. Chem. A 2009, 83, 254–259. doi:10.1134/S0036024409020186
Return to citation in text: [1] -
Chapyshev, S. V.; Korchagin, D. V.; Budyka, M. F.; Gavrishova, T. N.; Neuhaus, P.; Sander, W. J. Phys. Chem. A 2011, 115, 8419–8425. doi:10.1021/jp203038k
Return to citation in text: [1] -
Misochko, E. Ya.; Akimov, A. V.; Masitov, A. A.; Korchagin, D. V.; Yakushchenko, I. K.; Chapyshev, S. V. J. Chem. Phys. 2012, 137, No. 064308. doi:10.1063/1.4742342
Return to citation in text: [1] -
Chapyshev, S. V.; Grote, D.; Finke, C.; Sander, W. J. Org. Chem. 2008, 73, 7045–7051. doi:10.1021/jo800425k
Return to citation in text: [1] [2] [3] [4] [5] [6] [7] -
Misochko, E. Ya.; Akimov, A. V.; Chapyshev, S. V. J. Chem. Phys. 2008, 129, No. 174510. doi:10.1063/1.3005378
Return to citation in text: [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] -
Chapyshev, S. V.; Neuhaus, P.; Grote, D.; Sander, W. J. Phys. Org. Chem. 2010, 23, 340–346. doi:10.1002/poc.1622
Return to citation in text: [1] [2] [3] [4] [5] [6] [7] [8] -
Misochko, E. Ya.; Korchagin, D. V.; Bozhenko, K. V.; Chapyshev, S. V.; Aldoshin, S. M. J. Chem. Phys. 2010, 133, No. 064101. doi:10.1063/1.3474574
Return to citation in text: [1] [2] [3] [4] [5] -
Reiser, A.; Marley, R. Trans. Faraday Soc. 1968, 64, 1806–1815. doi:10.1039/TF9686401806
Return to citation in text: [1] -
Korchagin, D. V.; Bozhenko, K. V.; Chapyshev, S. V.; Aldoshin, S. M. High Energy Chem. 2009, 43, 289–293. doi:10.1134/S0018143909040080
Return to citation in text: [1] [2] [3] [4] -
Budyka, M. F.; Zyubina, T. S. J. Mol. Struct. 1997, 419, 191–199. doi:10.1016/S0166-1280(97)00244-3
Return to citation in text: [1] -
Budyka, M. F. Russ. Chem. Rev. 2008, 77, 709–723. doi:10.1070/RC2008v077n08ABEH003793
Return to citation in text: [1] -
Chapyshev, S. V. J. Fluorine Chem. 2011, 132, 991–994. doi:10.1016/j.jfluchem.2011.07.012
Return to citation in text: [1] -
Stoll, S.; Schweiger, A. J. Magn. Reson. 2006, 178, 42–55. doi:10.1016/j.jmr.2005.08.013
Return to citation in text: [1] -
Gaussian 03, Revision D.01; Gaussian, Inc.: Wallingford, CT, 2004.
Return to citation in text: [1] -
ORCA, an ab initio, density functional and semiempirical program package, Version 2.8.0.2; University of Bonn: Germany, 2011.
The program was downloaded from http://cec.mpg.de/forum/
Return to citation in text: [1] -
Neese, F. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2, 73–78. doi:10.1002/wcms.81
Return to citation in text: [1] -
Neese, F. J. Chem. Phys. 2007, 127, No. 164112. doi:10.1063/1.2772857
Return to citation in text: [1]
| 8. | Chapyshev, S. V.; Walton, R.; Lahti, P. M. Mendeleev Commun. 2000, 10, 187–188. doi:10.1070/MC2000v010n05ABEH001308 |
| 34. | Korchagin, D. V.; Bozhenko, K. V.; Chapyshev, S. V.; Aldoshin, S. M. High Energy Chem. 2009, 43, 289–293. doi:10.1134/S0018143909040080 |
| 34. | Korchagin, D. V.; Bozhenko, K. V.; Chapyshev, S. V.; Aldoshin, S. M. High Energy Chem. 2009, 43, 289–293. doi:10.1134/S0018143909040080 |
| 35. | Budyka, M. F.; Zyubina, T. S. J. Mol. Struct. 1997, 419, 191–199. doi:10.1016/S0166-1280(97)00244-3 |
| 36. | Budyka, M. F. Russ. Chem. Rev. 2008, 77, 709–723. doi:10.1070/RC2008v077n08ABEH003793 |
| 37. | Chapyshev, S. V. J. Fluorine Chem. 2011, 132, 991–994. doi:10.1016/j.jfluchem.2011.07.012 |
| 1. | Bräse, S.; Banert, K., Eds. Organic Azides: Synthesis and Applications; Wiley-VCH: Chichester, U.K., 2010. |
| 2. | Scriven, F. F. V., Ed. Azides and Nitrenes, Reactivity and Utility; Academic Press: New York, USA, 1984. |
| 3. | Bräse, S.; Gil, C.; Knepper, K.; Zimmermann, V. Angew. Chem., Int. Ed. 2005, 44, 5188–5240. doi:10.1002/anie.200400657 |
| 4. | Scriven, E. V. F.; Turnbull, K. Chem. Rev. 1988, 88, 297–368. doi:10.1021/cr00084a001 |
| 5. | Chapyshev, S. V. Synlett 2009, 1–8. doi:10.1055/s-0028-1087479 |
| 6. | Chapyshev, S. V. Russ. Chem. Bull. 2011, 60, 1274–1285. doi:10.1007/s11172-011-0195-7 |
| 10. | Chapyshev, S. V.; Korchagin, D. V.; Budyka, M. F.; Gavrishova, T. N.; Neuhaus, P.; Sander, W. ChemPhysChem 2012, 13, 2721–2728. doi:10.1002/cphc.201200200 |
| 29. | Chapyshev, S. V.; Grote, D.; Finke, C.; Sander, W. J. Org. Chem. 2008, 73, 7045–7051. doi:10.1021/jo800425k |
| 30. | Misochko, E. Ya.; Akimov, A. V.; Chapyshev, S. V. J. Chem. Phys. 2008, 129, No. 174510. doi:10.1063/1.3005378 |
| 31. | Chapyshev, S. V.; Neuhaus, P.; Grote, D.; Sander, W. J. Phys. Org. Chem. 2010, 23, 340–346. doi:10.1002/poc.1622 |
| 9. | Finke, C.; Grote, D.; Seidel, R. W.; Chapyshev, S. V.; Sander, W. J. Phys. Org. Chem. 2012, 25, 486–492. doi:10.1002/poc.1943 |
| 30. | Misochko, E. Ya.; Akimov, A. V.; Chapyshev, S. V. J. Chem. Phys. 2008, 129, No. 174510. doi:10.1063/1.3005378 |
| 7. | Chapyshev, S. V.; Walton, R.; Sanborn, J. A.; Lahti, P. M. J. Am. Chem. Soc. 2000, 122, 1580–1588. doi:10.1021/ja993131c |
| 8. | Chapyshev, S. V.; Walton, R.; Lahti, P. M. Mendeleev Commun. 2000, 10, 187–188. doi:10.1070/MC2000v010n05ABEH001308 |
| 30. | Misochko, E. Ya.; Akimov, A. V.; Chapyshev, S. V. J. Chem. Phys. 2008, 129, No. 174510. doi:10.1063/1.3005378 |
| 7. | Chapyshev, S. V.; Walton, R.; Sanborn, J. A.; Lahti, P. M. J. Am. Chem. Soc. 2000, 122, 1580–1588. doi:10.1021/ja993131c |
| 8. | Chapyshev, S. V.; Walton, R.; Lahti, P. M. Mendeleev Commun. 2000, 10, 187–188. doi:10.1070/MC2000v010n05ABEH001308 |
| 9. | Finke, C.; Grote, D.; Seidel, R. W.; Chapyshev, S. V.; Sander, W. J. Phys. Org. Chem. 2012, 25, 486–492. doi:10.1002/poc.1943 |
| 10. | Chapyshev, S. V.; Korchagin, D. V.; Budyka, M. F.; Gavrishova, T. N.; Neuhaus, P.; Sander, W. ChemPhysChem 2012, 13, 2721–2728. doi:10.1002/cphc.201200200 |
| 32. | Misochko, E. Ya.; Korchagin, D. V.; Bozhenko, K. V.; Chapyshev, S. V.; Aldoshin, S. M. J. Chem. Phys. 2010, 133, No. 064101. doi:10.1063/1.3474574 |
| 31. | Chapyshev, S. V.; Neuhaus, P.; Grote, D.; Sander, W. J. Phys. Org. Chem. 2010, 23, 340–346. doi:10.1002/poc.1622 |
| 30. | Misochko, E. Ya.; Akimov, A. V.; Chapyshev, S. V. J. Chem. Phys. 2008, 129, No. 174510. doi:10.1063/1.3005378 |
| 40. |
ORCA, an ab initio, density functional and semiempirical program package, Version 2.8.0.2; University of Bonn: Germany, 2011.
The program was downloaded from http://cec.mpg.de/forum/ |
| 41. | Neese, F. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2, 73–78. doi:10.1002/wcms.81 |
| 29. | Chapyshev, S. V.; Grote, D.; Finke, C.; Sander, W. J. Org. Chem. 2008, 73, 7045–7051. doi:10.1021/jo800425k |
| 30. | Misochko, E. Ya.; Akimov, A. V.; Chapyshev, S. V. J. Chem. Phys. 2008, 129, No. 174510. doi:10.1063/1.3005378 |
| 31. | Chapyshev, S. V.; Neuhaus, P.; Grote, D.; Sander, W. J. Phys. Org. Chem. 2010, 23, 340–346. doi:10.1002/poc.1622 |
| 31. | Chapyshev, S. V.; Neuhaus, P.; Grote, D.; Sander, W. J. Phys. Org. Chem. 2010, 23, 340–346. doi:10.1002/poc.1622 |
| 32. | Misochko, E. Ya.; Korchagin, D. V.; Bozhenko, K. V.; Chapyshev, S. V.; Aldoshin, S. M. J. Chem. Phys. 2010, 133, No. 064101. doi:10.1063/1.3474574 |
| 38. | Stoll, S.; Schweiger, A. J. Magn. Reson. 2006, 178, 42–55. doi:10.1016/j.jmr.2005.08.013 |
| 11. | Nimura, S.; Yabe, A. In Magnetic Properties of Organic Materials; Lahti, P. M., Ed.; Marcel Dekker: New York, 1999; pp 127–145. |
| 12. | Fukuzawa, T. A.; Sato, K.; Ichimura, A. S.; Kinoshita, T.; Takui, T.; Itoh, K.; Lahti, P. M. Mol. Cryst. Liq. Cryst. 1996, 278, 253–260. doi:10.1080/10587259608033683 |
| 13. | Kalgutkar, R. S.; Lahti, P. M. J. Am. Chem. Soc. 1997, 119, 4771–4772. doi:10.1021/ja963723k |
| 14. | Chapyshev, S. V.; Walton, R.; Lahti, P. M. Mendeleev Commun. 2000, 10, 114–115. doi:10.1070/MC2000v010n03ABEH001281 |
| 15. | Miura, Y.; Oka, H.; Teki, Y. Bull. Chem. Soc. Jpn. 2001, 74, 385–386. doi:10.1246/bcsj.74.385 |
| 16. | Kalgutkar, R. S.; Lahti, P. M. Tetrahedron Lett. 2003, 44, 2625–2628. doi:10.1016/S0040-4039(03)00385-X |
| 17. | Chapyshev, S. V.; Tomioka, H. Bull. Chem. Soc. Jpn. 2003, 76, 2075–2089. doi:10.1246/bcsj.76.2075 |
| 18. | Sato, T.; Narazaki, A.; Kawaguchi, Y.; Niino, H.; Bucher, G.; Grote, D.; Wolff, J. J.; Wenk, H. H.; Sander, W. J. Am. Chem. Soc. 2004, 126, 7846–7852. doi:10.1021/ja031794v |
| 19. | Chapyshev, S. V.; Walton, R.; Serwinski, P. R.; Lahti, P. M. J. Phys. Chem. A 2004, 108, 6643–6649. doi:10.1021/jp048764e |
| 20. | Chapyshev, S. V.; Lahti, P. M. J. Phys. Org. Chem. 2006, 19, 637–641. doi:10.1002/poc.1106 |
| 21. | Chapyshev, S. V. Russ. Chem. Bull. 2006, 55, 1126–1131. doi:10.1007/s11172-006-0388-7 |
| 22. | Chapyshev, S. V. Russ. Chem. Bull. 2006, 55, 1593–1597. doi:10.1007/s11172-006-0459-9 |
| 23. | Misochko, E. Ya.; Akimov, A. V.; Chapyshev, S. V. J. Chem. Phys. 2008, 128, No. 124504. doi:10.1063/1.2840351 |
| 24. | Koto, T.; Sato, K.; Shiomi, D.; Toyota, K.; Itoh, K.; Wasserman, E.; Takui, T. J. Phys. Chem. A 2009, 113, 9521–9526. doi:10.1021/jp9042717 |
| 25. | Chapyshev, S. V.; Misochko, E. Ya.; Akimov, A. V.; Dorokhov, V. G.; Neuhaus, P.; Grote, D.; Sander, W. J. Org. Chem. 2009, 74, 7238–7244. doi:10.1021/jo9010848 |
| 26. | Chapyshev, S. V. Russ. J. Phys. Chem. A 2009, 83, 254–259. doi:10.1134/S0036024409020186 |
| 27. | Chapyshev, S. V.; Korchagin, D. V.; Budyka, M. F.; Gavrishova, T. N.; Neuhaus, P.; Sander, W. J. Phys. Chem. A 2011, 115, 8419–8425. doi:10.1021/jp203038k |
| 28. | Misochko, E. Ya.; Akimov, A. V.; Masitov, A. A.; Korchagin, D. V.; Yakushchenko, I. K.; Chapyshev, S. V. J. Chem. Phys. 2012, 137, No. 064308. doi:10.1063/1.4742342 |
| 29. | Chapyshev, S. V.; Grote, D.; Finke, C.; Sander, W. J. Org. Chem. 2008, 73, 7045–7051. doi:10.1021/jo800425k |
| 30. | Misochko, E. Ya.; Akimov, A. V.; Chapyshev, S. V. J. Chem. Phys. 2008, 129, No. 174510. doi:10.1063/1.3005378 |
| 31. | Chapyshev, S. V.; Neuhaus, P.; Grote, D.; Sander, W. J. Phys. Org. Chem. 2010, 23, 340–346. doi:10.1002/poc.1622 |
| 29. | Chapyshev, S. V.; Grote, D.; Finke, C.; Sander, W. J. Org. Chem. 2008, 73, 7045–7051. doi:10.1021/jo800425k |
| 30. | Misochko, E. Ya.; Akimov, A. V.; Chapyshev, S. V. J. Chem. Phys. 2008, 129, No. 174510. doi:10.1063/1.3005378 |
| 31. | Chapyshev, S. V.; Neuhaus, P.; Grote, D.; Sander, W. J. Phys. Org. Chem. 2010, 23, 340–346. doi:10.1002/poc.1622 |
| 21. | Chapyshev, S. V. Russ. Chem. Bull. 2006, 55, 1126–1131. doi:10.1007/s11172-006-0388-7 |
| 29. | Chapyshev, S. V.; Grote, D.; Finke, C.; Sander, W. J. Org. Chem. 2008, 73, 7045–7051. doi:10.1021/jo800425k |
| 30. | Misochko, E. Ya.; Akimov, A. V.; Chapyshev, S. V. J. Chem. Phys. 2008, 129, No. 174510. doi:10.1063/1.3005378 |
| 31. | Chapyshev, S. V.; Neuhaus, P.; Grote, D.; Sander, W. J. Phys. Org. Chem. 2010, 23, 340–346. doi:10.1002/poc.1622 |
| 29. | Chapyshev, S. V.; Grote, D.; Finke, C.; Sander, W. J. Org. Chem. 2008, 73, 7045–7051. doi:10.1021/jo800425k |
| 32. | Misochko, E. Ya.; Korchagin, D. V.; Bozhenko, K. V.; Chapyshev, S. V.; Aldoshin, S. M. J. Chem. Phys. 2010, 133, No. 064101. doi:10.1063/1.3474574 |
| 10. | Chapyshev, S. V.; Korchagin, D. V.; Budyka, M. F.; Gavrishova, T. N.; Neuhaus, P.; Sander, W. ChemPhysChem 2012, 13, 2721–2728. doi:10.1002/cphc.201200200 |
| 8. | Chapyshev, S. V.; Walton, R.; Lahti, P. M. Mendeleev Commun. 2000, 10, 187–188. doi:10.1070/MC2000v010n05ABEH001308 |
| 34. | Korchagin, D. V.; Bozhenko, K. V.; Chapyshev, S. V.; Aldoshin, S. M. High Energy Chem. 2009, 43, 289–293. doi:10.1134/S0018143909040080 |
| 24. | Koto, T.; Sato, K.; Shiomi, D.; Toyota, K.; Itoh, K.; Wasserman, E.; Takui, T. J. Phys. Chem. A 2009, 113, 9521–9526. doi:10.1021/jp9042717 |
| 33. | Reiser, A.; Marley, R. Trans. Faraday Soc. 1968, 64, 1806–1815. doi:10.1039/TF9686401806 |
| 34. | Korchagin, D. V.; Bozhenko, K. V.; Chapyshev, S. V.; Aldoshin, S. M. High Energy Chem. 2009, 43, 289–293. doi:10.1134/S0018143909040080 |
| 30. | Misochko, E. Ya.; Akimov, A. V.; Chapyshev, S. V. J. Chem. Phys. 2008, 129, No. 174510. doi:10.1063/1.3005378 |
| 32. | Misochko, E. Ya.; Korchagin, D. V.; Bozhenko, K. V.; Chapyshev, S. V.; Aldoshin, S. M. J. Chem. Phys. 2010, 133, No. 064101. doi:10.1063/1.3474574 |
| 32. | Misochko, E. Ya.; Korchagin, D. V.; Bozhenko, K. V.; Chapyshev, S. V.; Aldoshin, S. M. J. Chem. Phys. 2010, 133, No. 064101. doi:10.1063/1.3474574 |
| 29. | Chapyshev, S. V.; Grote, D.; Finke, C.; Sander, W. J. Org. Chem. 2008, 73, 7045–7051. doi:10.1021/jo800425k |
| 30. | Misochko, E. Ya.; Akimov, A. V.; Chapyshev, S. V. J. Chem. Phys. 2008, 129, No. 174510. doi:10.1063/1.3005378 |
| 31. | Chapyshev, S. V.; Neuhaus, P.; Grote, D.; Sander, W. J. Phys. Org. Chem. 2010, 23, 340–346. doi:10.1002/poc.1622 |
© 2013 Chapyshev et al; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The license is subject to the Beilstein Journal of Organic Chemistry terms and conditions: (http://www.beilstein-journals.org/bjoc)